Dear reader, believe it or not, this is actually a post about mathematics. A Christian parable will be exaggerated for comedic effect to explain a mathematical concept. I have the utmost respect for Christianity. Do not read any further meanings into the presentation. Content in square brackets mean they do not have a bearing on the main story.
This post is about mathematics. Precisely, it is about lines. So feel free to skip it. But I would really like you to read it regardless so maybe don’t stop, please? As a mathematician, it is often in our character to obsess over something that is seemingly insignificant such as a line. World hunger is a big problem, right? What is a line in comparison to that? I could argue that knowing a lot about lines contributes to solving that problem. It is indeed factual, and I wouldn’t be lying. However, the best answer is this: it doesn’t matter. We all have our parts to play in this world. In what follows, I will draw a connection between a famous parable told by none other than Jesus Christ himself and, dare I say, lines, or curves, if you like. For most intents and purposes, we regard them as the same in mathematics. The conclusion might shock or bore you. Let’s dive in!
What is a line?
In mathematics, it is often desirable to have a line or a curve that has no breaks in them. If you could imagine how important lines are in mathematics, then it is not a stretch of the imagination to accept that lines that don’t break could be even more important. At this point, you might be reading and thinking, that is a ‘you’ problem. How should lines be important to me a non-mathematician? Well, lines are used to model the behaviour of things in the real world where [Surprise!] we both live. They have the ability to minimise focus on an object—because we won’t even show that particular object—and tell us where that object has been, and where it is going instead. You can imagine a line to be the trajectory of a series of dots. Every dot represents the position of some arbitrary object, which we don’t care about presently, at a particular instance in time. You can think on that for a second. Here are some instantly recognisable mathematical lines:
The beating of your heart and the way light particles actually look like is what we call a wave. When you throw a ball, or launch a rocket, mathematics and physics people just describe it as the motion of a projectile.
Forget about the basketball for a second, and focus on the path its movement is tracing. That is what we are talking about.
Of course the lines alone don’t tell the whole story. Look at the picture of the light waves above. You have to have some ‘map’ on which the line lies. [Forgive the unnecessary use of the alliteration. I couldn’t help it!] This map tells you exactly what the line is trying to communicate to you. The background map would probably have some axes, most likely two of them, and some numbers on the axes. These numbers would have to be equally spaced on each axis even though the particular length of space for each axis doesn’t have to be the same. That map plus the line is called a graph. Perhaps you have heard about it?
Story time
In the sixteenth chapter of the gospel of Luke, Jesus told the Pharisees and those who were gathered a story. And you know his stories read exactly like how those European painters depicted the things he did: so unbelievably terse! I mean he wasn’t trying to be an award-winning novelist but, still, the plots needed some work. [Dear reader, please do not take offence. I am only joking.] If you don’t believe me, picture the story I am about to narrate.

There was a wealthy man who lived the way wealthy men supposedly did: he ate like a god and dressed like a peacock. It could be he had some odd hobbies as well. But contrary to most rich capitalist men these days, he wasn’t philanthropic at all. Like, zero! [He did not set up a foundation to help the (…). You get the idea.] So there was this extremely poor dude called Lazarus with god-awful skin diseases who wanted to eat the leftovers from his table. [The diseases were most probably caused by not having access to baths. You would not believe how difficult it was to get regular baths those days. Look it up!] It was so bad dogs came to lick the sores on his body. The bible says he was a beggar. The next part is a bit fuzzy on the details so bear with me. It does seem the rich man prepared lots of food every time and threw away his leftover food constantly. Maybe instead of giving it out to the less fortunate he just threw them in the garbage? Or, maybe he intentionally ruined the food so it couldn’t be eaten? I don’t know. I don’t even know how Lazarus was stomach-watching the guy. How does he even know what the rich man ate and what-not? Did Lazarus just hear about it from other people? Jesus makes it seem like he actually goes to call Lazarus every time he wants to eat. And then, he takes his time to sink his teeth into his chicken and makes eye contact with Lazarus as he chews. That would be cruel! Anyway, let’s get off that tangent. So wealthy man dies. It wasn’t a big deal: a wealthy man who was not sympathetic to the plight of the poor had died. It happens everyday. Around the same time (probably?), the piss poor dude also kicked the bucket.
So naturally (of course), the poor man goes to a place that is only described in the bible as Abraham’s bosom. [Interesting fact: it is not definitively known where Abraham’s bosom actually is but there are many theories.] The ‘rich, cruel’ man descends to Hades. [I do not like to use the term Hell because of some connotations I cannot get into.] You could say that he wasn’t exactly comfortable there. He screamed to Abraham and directs him to send Lazarus to bring him a drop of water on Lazarus’s fingertip. Of course, he did. Even in death, he seems out of touch with reality and defaults to his privilege. What is interesting to me is the setup of that universe: there is Hades, Abraham’s bosom and a great chasm between the two places. And even though there is a huge gulf between the two worlds, they could still communicate. Isn’t that fascinating? The wealthy man was so close to the bosom of his father Abraham, and yet so far. You couldn’t cross the space between Hades and Abraham’s bossom. However, you could infer that they are in the same universe, seeing as people from both places were speaking to each other. I would like to use that universe to teach something cool in mathematics! Excited yet?
Limits
In calculus, which is an aspect of mathematics, there is something called a smooth function. A smooth function can actually be represented with some graph of a line. So really, a graph is a pictorial representation of a function. We are saying that when you look at a graph that represents a smooth function, its line has no break in it. In addition to this, we would like the line to have no sharp turns (like the ones for heart wave). There are different kinds of breaks, or as mathematicians like to call them, discontinuities. But we would like to focus on the type pictured below:
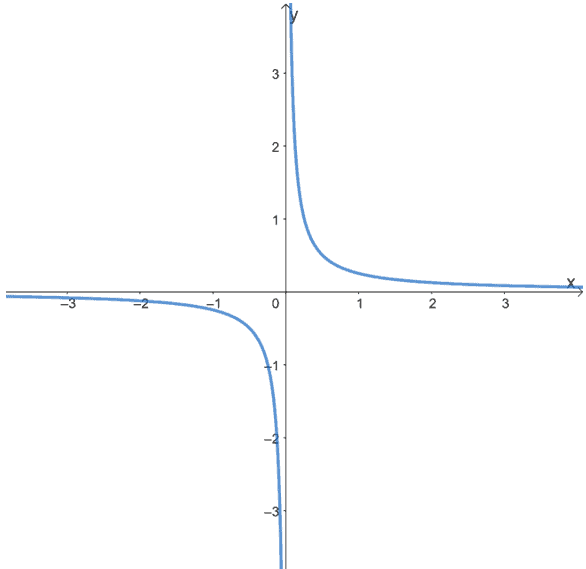
If you look closely enough, you can see the parallels between the graph and the ghastly story told by Jesus. Both Hades and Abraham’s bossom appear to be in the same universe. So even though we can see two different lines, they are really the graph of one function $y=f(x)= \frac{1}{x}$. You will notice that the origin, that is, the single point $x=y=0$ seems to be repelling the two lines. Mathematically speaking, the two lines could meet if not for the pesky origin point $0$. They are so close, and yet so far. There seems to be so little separating them. But if you were a point on either line, you would not see it that way: just like how you can see things on a scale an ant couldn’t dream of. If you are a point who is condemned to move on the path traced by those two lines (that is, either you are Lazarus or the Rich Man), you will never be able to reach $0$. There will be a distance between the two lines that you cannot reconcile no matter what.
What is causing this mathematically, you ask? The answer has to do with the so-called limit of the function $y=\frac{1}{x}$ as $x$ approaches the origin $0$. The limit for the particular function pictured is infinity! Its symbol is $\infty$. Well, it actually evaluates to two types infinities depending on where you are approaching the origin from: negative or positive. Let us start with the mathematical definition for a limit. Let $f(x)$ be a single-valued function. The limit $L$ of a function $f(x)$ as $x$ approaches a certain point, say $p$, is written like this: \[\lim_{x\rightarrow p} f(x) = L\] Let us dismantle this mumbo-jumbo. First, picture a function $f$. It is simply a rule that takes an input value $x$ and spits an out output value $f(x)$.
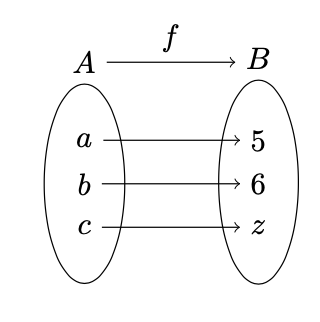
The space where the input values are found is called the domain. Likewise, the space where the output values are found is known as the codomain. Limits are really about how a function behaves near a particular input. Now picture the above function as some smooth function. Pick a particular point $p$. Suppose that $f(x)$ gets closer and closer to some functional value $L$ as $x$ moves closer and closer to $p$. Then $L$ is the limit of the function $f(x)$. Put another way, if two points are close to each other in the domain, it means they will be close once again when they are mapped by the function to the codomain. If you really think about it, this is what creates the ‘illusion’ of smoothness of a function! Practically, you ensure this criteria by looking at both directions of approaching the point in question. This is best illustrated with an example.
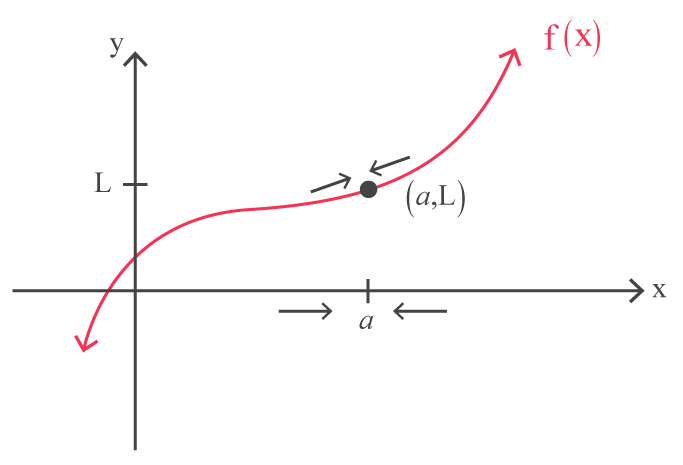
This is called one sided limit. To ensure there is truly a limit, the limit when you approach a point from either side of the line must coincide. That is, mathematically \[\lim_{x\rightarrow a^-} f(x) = \lim_{x\rightarrow a^+} f(x) = L.\] The limit on the left is called the left hand limit and that on the right is called the right hand limit. If at any point the limit of the function is not the same when approached from both the left and right sides, we say the limit does not exist.
There is a caveat though. When we are speaking about limit of a function at a point, we don’t actually care about the functional value at that point. Let us assume that $M=f(a)$, which is the output value of the function $f$ at the point $a$, does not exist. We can still speak about the limit of the function at that particular point. We do not need the functional value to exist.
Look at the function directly above. There is a hole in the line at $x=0$. This means that the function is not defined at that particular point. You could also say that the part in the circle is not part of the function. However, the function still has a limit at that point.
Let us go back to our original function $f(x) = \frac{1}{x}$. Here is the table of values as the function approaches $0$ from the left:
| $x$ | $-0.4$ | $-0.3$ | $-0.2$ | $-0.1$ | $-0.01$ | $-0.001$ | $-0.0001$ |
|---|---|---|---|---|---|---|---|
| $\frac{1}{x}$ | $-2.5$ | $-3.3333$ | $-5$ | $-10$ | $-100$ | $-1000$ | $-10000$j |
Wejhave just tabulated that \[\lim_{x\rightarrow 0^-} \frac{1}{x} = -\infty.\] We can clearly see that it starts to get weird near $0$: the numbers start to blow up. Same thing applies to the values as the function approaches $0$ from the right:
| $x$ | $0.4$ | $0.3$ | $0.2$ | $0.1$ | $0.01$ | $0.001$ | $0.0001$ | $0.00001$ |
|---|---|---|---|---|---|---|---|---|
| $\frac{1}{x}$ | $2.5$ | $3.3333$ | $5$ | $10$ | $100$ | $1000$ | $10000$ | $100000$ |
That also shows the following: \[\lim_{x\rightarrow 0^+} \frac{1}{x} = \infty.\] As we get close to $0$, we realise that the values the function gets really big, and they continue to get bigger without any bounds. Hence, we symbolise this as the limit of the function approaching near $0$.
Takeway?
The chasm between Hades and Abraham’s bossom is fascinating. Even though it is wide enough that people in either realms cannot cross over to the other, people seem to be able to talk to each other quite fine. Just imagine it. Someone is so close to you that you can hear them when they whisper. And yet, you cannot physically be in the same space with them. You cannot touch the other person no matter how hard you try. We use this idea to explore to illustrate why \[\lim_{x\rightarrow 0}\frac{1}{x} = \infty.\] When that happens, we say that the limit of said function as $x$ approaches $0$ does not exist.
](/assets/images/sinx-over-x.svg)